Geometry Patterns in Python

Python generator functions are a great way to make procedural patterns!

In this article, you'll see some examples of how to draw gears, spirals, stars and more using Python.

In case you don't know how generator functions work, they are a bit like regular functions, but instead of "return" you use "yield". When you yield a value, the function outputs that value, and when you iterate or call next() on the generator, the function begins not at the beginning, but directly after the previous yield command.

It's like a bookmark, and you pick up right where you left off.

Generators are usually talked about in terms of being memory efficient. Iterating over large datasets. But that isn't what we're here to talk about today.

A lot of the time, I'll create a generator, but still have to flatten it out into a list to pass to another command. For example, the curve() command in Maya takes a list of points. Or the appendPoly() command in the TouchDesigner scriptSOP needs to know how many points your poly will have in advance. Generators are like a stream, so if you want to count the total output, you need to convert it to a list.

But oh well. Even if you have to give up the memory benefits of a generator, I find that the yield pattern is very intuitive for creating geometric or repetitive patterns! Your patterns dive in and out of the function, like threading a needle.

This isn't the only way to make shapes. Probably not even the best way. But I find it fun and intuitive and iterative.

Here is some procedural art I created using this technique. The curve segments are generated in Python using variations on the functions below.

Polar spirals night mode! Coded in #python and rendered with #TouchDesigner. #generativeart #creativecoding #procedural

A post shared by Chris Lesage (@rigmarolestudio) on Apr 16, 2018 at 6:40pm PDT

The base curves look something like this before rendering and compositing.

Here are some shapes with Python examples.

Note that the following code examples won't draw anything. They will just generate points. You'll then have to take those points and put them into your own graphics library or 3D program to draw the lines. You could use the curve() command in Maya. Or the Python SOP in Houdini or script SOP in TouchDesigner. Or some web graphics library. It's up to you!

First, I'm going to set up a couple of helper functions. One to lerp (linear interpolate) values. Another to turn polar coordinates into cartesian coordinates. This lets you easily set points around a circle shape.

import math

def polar_to_cartesian(theta, radius):
        return (0.0, math.cos(theta)*radius, math.sin(theta)*radius)
        

def lerp_values(lower, upper, segments, inclusive=True):
    ''' lerp values and optionally include the first and last values '''
    for each in range(segments):
        if each in [0, segments-1] and not inclusive:
            pass
        else:
            yield (each / float(segments-1)) * (float(upper)-float(lower)) + lower

Sawtooth Wave

def sawtooth_wave_pattern(height, width, segments):
    """ Create a generator of points that make a saw-tooth wave shape |_|⎺|_|⎺|_|⎺|_|⎺| """
    heightPoints = [1.0 * height, -1.0 * height]
    segmentRange = range(-segments, segments+1)
    widthPoints = [(x/float(segments) * width) for x in segmentRange]

    for each, each2 in zip(widthPoints[0::2], widthPoints[1::2]):
        # DOWN
        yield [0.0, heightPoints[0], each]
        yield [0.0, heightPoints[1], each]
        # UP
        yield [0.0, heightPoints[1], each2]
        yield [0.0, heightPoints[0], each2]
    # to finish the wave, add the final DOWN cycle
    yield [0.0, heightPoints[0], widthPoints[-1]]
    yield [0.0, heightPoints[1], widthPoints[-1]]

sawtooth_wave_pattern(4.0, 6.0, 15)

Gears

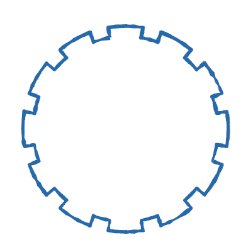
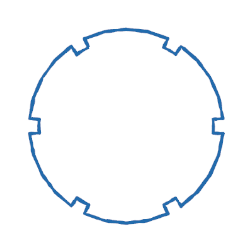
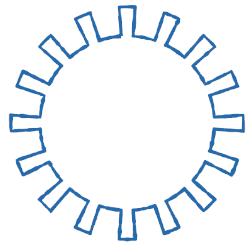
This one is a bit more complex. But writing it was still a very iterative process.

def gear_pattern(gears, inner_radius, outer_radius, gear_ratio):
    """
    Draw gears. Lerp an arc until a segment is complete. Then lerp in or out.
    Includes an option for the size ratio between teeth and notches
    """
    
    arc_samples = 5
    notch_samples = 5
    
    # each gear has a corresponding notch. So multiply times 2.
    gear_width = math.pi*2.0 / gears
    # the width range of a gear or notch can be from 0 to 2 segments.
    # For example, if the gear was 2 segments wide, the notch would be 0.
    inner_width = (1 - gear_ratio) * (gear_width)
    outer_width = gear_ratio * (gear_width)
    
    # multiply the width so the first gear is centered at the top
    arc1 = 0 + (outer_width * 0.5)
    arc2 = inner_width  + (outer_width * 0.5)
    
    for gear in range(gears):
        # draw the inner notch
        for lerp in lerp_values(arc1, arc2, arc_samples, inclusive=True):
            yield polar_to_cartesian(lerp, inner_radius)
        # draw outwards
        for lerp in lerp_values(inner_radius, outer_radius, notch_samples, inclusive=False):
            yield polar_to_cartesian(arc2, lerp)
        arc1 += inner_width
        arc2 = arc1 + outer_width
        
        # draw the outer edge of the tooth
        for lerp in lerp_values(arc1, arc2, arc_samples, inclusive=True):
            yield polar_to_cartesian(lerp, outer_radius)
        # draw inwards
        for lerp in lerp_values(outer_radius, inner_radius, notch_samples, inclusive=False):
            yield polar_to_cartesian(arc2, lerp)
        arc1 += outer_width
        arc2 = arc1 + inner_width
    
    # cap off the shape if needed, by drawing another point at the original 0 point.
    yield polar_to_cartesian(0 + (outer_width * 0.5), inner_radius)

gear_pattern(12, 4.5, 4.0, 0.25)
gear_pattern(6, 4.5, 4.0, 0.25)
gear_pattern(16, 4.5, 6.0, 0.35)

Spirals

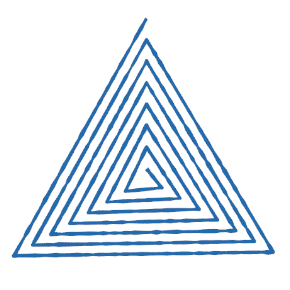
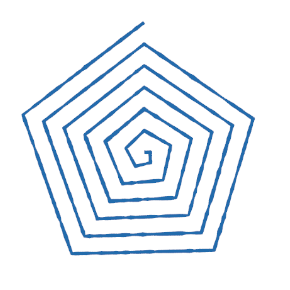
def spiral_pattern(loops, startRadius, endRadius, density):
    startRadius = float(startRadius)
    endRadius = float(endRadius)
    segments = loops*density+1
    arcRange = [arc/float(segments-1) * math.pi * 2.0 for arc in range(int(segments))]
    for i, lerp in enumerate(lerp_values(startRadius, endRadius, int(segments), inclusive=True)):
        yield polar_to_cartesian(-arcRange[i]*loops, lerp)

spiral_pattern(12, 0.1, 5.0, 40)
spiral_pattern(7, 0.1, 5.0, 3)
spiral_pattern(6, 0.1, 5.0, 5)

Sine wave

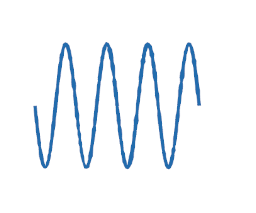
def sine_wave_pattern(loops, width, height, density):
    maxWidth = (math.pi*2.0) * loops
    for loop in range(loops):
        for lerp in lerp_values(0, math.pi*2, density, inclusive=True):
            # lerp to 2pi, then divide by maxWidth to normalize.
            # Then multiply to set the width.
            zpos = ((lerp+(loop*math.pi*2)) / maxWidth) * width
            ypos = math.sin(lerp)*height
            yield [0, ypos, zpos]

sine_wave_pattern(4, 8.0, 3.0, 40)

Star pattern

def star_pattern(points, innerRadius, outerRadius):
    radiusChoice = [outerRadius, innerRadius]
    switch = 0
    segments = math.pi * 2.0
    # I do this to shift the segments by half
    for lerp in lerp_values(0, segments, points*2+1, inclusive=True):
        yield polar_to_cartesian(lerp, radiusChoice[switch])
        switch = -switch + 1

star_pattern(5, 2.88, 5.0)
star_pattern(3, 5.0, 1.5)
star_pattern(4, 2.5, 5.0)
star_pattern(20, 5.0, 6.0)

All of these examples output points in cartesian space. But you could also use this when generating procedural polygon patterns, UV coordinates or repetitive patterns and templates in text or other data structures.

Thanks for reading!